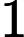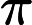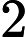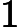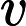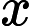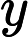Calculating Pi

If you're unsure what this is about, watch this awesome video that explains everything. You can find the code for this simulation on github.

But let me explain the setup here anyway. So, you have two blocks on a frictionless surface free to move in one direction.

The small block has \(1\) unit mass. The bigger block has mass of some power \(n\) of \(100\) units. And for the reason that is very well explained in the above linked video, the number of total collisions that happen before both the mass slide towards infinity never to interact again - that number comes out to be a whole number with first \(n\) digits of \(\pi\).

Small mass: 1 Kg
Big mass: 100 Kg

Collisions: 0

On conservation of Energy

It's clear that the total kinetic energy in the system is conserved. To put that in equations:

where, the symbols have the usual meaning. \(E\) is constant and its exact value isn't relevant for our problem since the result (i.e. total number of collisions) is the same irrespective of the initial velocity of the bigger block.

Since, only \(v_1\) and \(v_2\) are changing in the above equation, it makes sense to try to plot the equations with those as the coordinates.

You can immediately see that the equation is an ellipse. We can transform it to a circle if we scale the coordinate axes by right amount - in particular if we take \(x = \sqrt{m_1}v_1\) and \(y = \sqrt{m_2}v_2\) as the coordinates.

That is what we've done in the diagram above. State of the system on this phase diagram, which is represented by black dots, changes on each collision. But it always remains on the circle. And we know that conservation of the energy is the reason why!

Make sure you're working with \(2\) digits to see the plot on phase space. Anything more than that would just cover up the entire circle because there are too many collisions. I've excluded those cases.