On trying to model spacetime

I've committed all sorts of mathematical sins with this post. This is just supposed to be a very very quick rundown of mathematical preliminaries that forms the basis of spacetime in the general theory of relativity.

Lengths, area, volume, curvature, rate of change etc are some of the things that we are interested to study in geometry. We have a good handle on those when the underlying space is nice and flat Euclidean. We are interested to extend this ability to spaces that are not Euclidean. As a physicist, we are interested to model spacetime mathematically. And if we are Einstein, we might be looking to allow it a curvature and hope it somehow encodes gravitation. Differential geometry is our attempt to model such physical reality in all mathematical rigour without being too restrictive.

At the coarsest level, spacetime is a set. It's a set of points. Let's call this set \(M\). Does a set so defined have enough complexity to model spacetime? Of course not. In fact, let's see what we have. A set is just an unordered collection of elements.

Imagine a sheet of paper to be some kind of two dimensional spacetime. Now, shred this sheet into pieces. That's not enough, collect all the pieces and grind them into fine powder, finest you can imagine. Finally, give it a good shuffle and that's what we have so far as a mathematical model of this paper sheet spacetime. We can see that the immediate next thing we want to have is some notion of locality or neighborhood meaning we want to be able to capture the idea that some points are "close" to each other.

So, we introduce a new set and give it a fancy name topology. A topology on a set is just a set which contains a whole bunch of sets as its elements, each of which defines a "locality". So, for each point \(p \in M\), there could be an entry in this set, denoted by \(\mathcal O\), which contains all the neighbour points of \(p\).

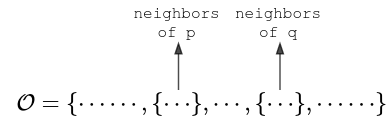
This gives us a way to put the powder together and give it a structure in some sense. But there are a lot of ways we could do it. In fact, it turns out the kind of topology that one can form given the restrictions we have so far are so many that most of them resemble the spacetime as we know it too little, whatever that means.

We look at a special kind of them called topological manifolds. Topological manifolds are topological space that can be charted similar to how surface of earth can be charted to a map on a plane sheet of paper. So, we require a condition that our model of spacetime be mapped continuously to subset of \(\mathbb R^n\). This essentially requires that there exist neighborhood to every point \(p \in M\) and for every neighborhood that its image can have in the chart.

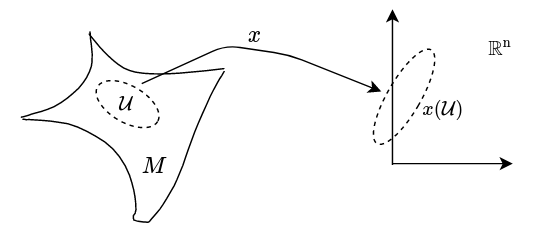
So, we now add one more information to our collection namely an Atlas denoted by \(\mathcal A\) which is a collection of charts \((\mathcal U, \mathcal x)\) where \(\mathcal U \subseteq M\) is a portion of the manifold that is covered in this particular chart and \(x\) is the map that takes \(\mathcal U\) to a portion \(\mathcal{x(U)} \subseteq \mathbb R^n\). We have a whole bunch of charts in the atlas because a single might not cover the entire manifold. So, we now consider only those spaces that are locally Euclidean.

A paper spacetime as a topological manifold, is closer to what we want compared to the powder that we had earlier. But you can still take the paper, crumple it with your hand and give it wrinkles and creases. You can even stretch, twist and turn and do all sorts of crazy thing with it. You could stretch it along one side and make a wire out of it. It doesn't care. It's still the same in our model.

You might say, stretching and squeezing is a property that we want to have in our model, afterall that's what we want to model gravitation with and you're right. We dont get rid of this flexibility. But we should be able to distinguish between two configurations. We want a notion of curvature. From Euclidean geometry, we know that curvature can be defined by employing second derivatives. We don't know how to do differentiation in a manifold yet.

The idea here is to do calculus in charts, where we have all nice results and theorems from analysis. But, immediately a question arises: will the results we get in charts will be well-defined? Because, one could just as easily go and look at another chart. The condition that holds in a chart that lead us to ascribe certain property on our manifold may not hold in another chart. This is very serious. We don't want the velocity of a particle, curvature of a trajectory and so on to depend on the choice of our coordinates (which is what charts really are).

So, let's think this through. Let's say we want to establish whether a certain curve on a manifold (this could be a particle trajectory) is continuous. We can go to a chart \((\mathcal U, \mathcal x)\) and check for the continuity of the chart representative of the curve. But the problem is when we have another chart \((\mathcal V, \mathcal y)\) and the two charts have some overlap. Now, in this overlap, the chart representatives of the curve better agree on their continuity.

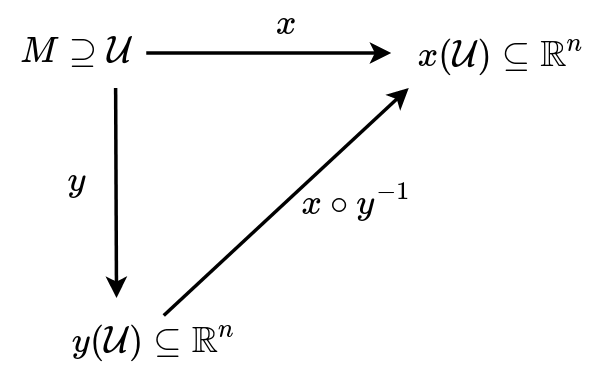
Now, there are 3 maps of interest here namely \(x\), \(y\), and \(x\circ y^{-1}\). We know from analysis, that a continuous curve in \(\mathbb R^n\) to remain continuous after a map, it suffices that the map be continuous. Therefore, we know that we need \(x\circ y^{-1}\) to be continuous. But, we also know that composition of two continuous functions is continuous. So, the continuity of chart maps and their inverses come to rescue and our definition of continuity that involves going to a chart remains well defined.

That was lucky. But what about differentiability? Can we define differentiability of curves and functions in the same way - by going to charts? Well, you cant make the same arguments about differentiability(chart maps are merely continuous and continuous maps may not be differentiable). So, the answer is no. We can't define differentiability without some further restrictions on our atlas.

And believe it or not, what we do is restrict our atlas such that chart transition map between any pair of overlapping charts is infinitely differentiable or in other word smooth. With that restriction, we now have a smooth manifold \((M, \mathcal{O, A})\) where we can do calculus without running into ill definition.

There is more to it, of course. For example, we haven't defined a metric yet. So, we can't talk about lengths and angles like we always had on flat Euclidean space. It's not clear how one could define derivatives and so on without a notion of length. We'll stumble upon a major hurdle in defining derivatives of tensor fields. I will talk about these in upcoming posts if I get the clarity and a way to avoid too much maths.